Читать книгу Радиус наблюдаемой Вселенной и горизонт Вселенной - Петр Путенихин - Страница 2

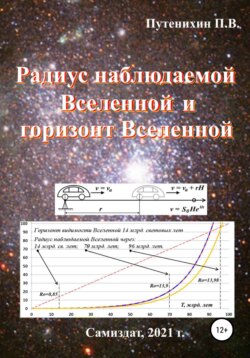
Рассмотрим это явление подробнее. Для наглядности и упрощения вычислений вместо сверхновой и расширяющегося пространства Вселенной рассмотрим автомобиль, движущийся по непрерывно вытягивающейся трассе (рис.10.1). Пусть авто движется со скоростью v_а по резиновой дорожке, которая растягивается, увеличиваясь за каждый фиксированный интервал времени Δt = t в е^Ht раз, где H – некоторая постоянная. В начальный момент времени авто находится на удалении S₀ от конечной точки, от финиша. Условно принимаем, что движение авто и расширение дорожки происходят поочерёдно. Находим, что за первый интервал времени авто переместится от начальной точки на расстояние

Пусть авто движется со скоростью v_а по резиновой дорожке, которая растягивается, увеличиваясь за каждый фиксированный интервал времени Δt = t в е^Ht раз, где H – некоторая постоянная. В начальный момент времени авто находится на удалении S₀ от конечной точки, от финиша.

Рис.10.1

Условно принимаем, что движение авто и расширение дорожки происходят поочерёдно. Находим, что за первый интервал времени авто переместится от начальной точки на расстояние

После этого отрезок R₀, путь, пройденный по дорожке, испытывает указанное расширение. Таким образом, за следующие два интервала времени удалённость авто от начальной точки увеличивается до нового значения

За четвёртый и пятый интервалы времени расстояние позади авто вновь возрастает, теперь уже до величины

Далее этот новый формально пройденный интервал R₃, длина дорожки "позади" за следующую пару интервалов времени возросла до следующего нового значения

Здесь и в дальнейшем открывающие скобки в левой части уравнения мы не будем дублировать, чтобы не перегружать уравнение, просто помним, что число крайних левых скобок равно числу правых скобок.

Для удобства, наглядности ограничимся на этом этапе десятью слагаемыми. Теперь для ещё большей наглядности уравнения последовательно раскроем скобки:

Число слагаемых, как мы и рассчитывали, равно 10, но число интервалов времени больше – 19. Понятно, что общее время движения T равно сумме всех интервалов Δt = t, поэтому можно записать T = (2n-1)t. Здесь мы учитываем, что все интервалы времени равны. Выносим общий множитель за скобки, а последнее слагаемое преобразуем в однотипную форму, добавив ему эквивалентный множитель, равный единице:

Для лучей видимости закономерности меняем последовательность слагаемых на противоположную:

Закономерность очевидна, поэтому можем записать уравнение в общем виде для любого количества интервалов времени и числа слагаемых:

Рассмотрим особый случай: авто достигает конечной точки, финиша. Это значит, что рассматриваемое уравнение, сумма ряда будет равна увеличившейся по указанному закону исходной дистанции, растягивающейся трассы. Поскольку начальная удалённость финиша была S₀, то через время T она увеличится до значения:

Рассматриваемое условие запишем в виде:

Перепишем правое равенство немного короче, в одну строку:

Для графических построений удобнее немного иная форма записи правой части уравнения, в виде, напоминающем исходное уравнение со множеством скобок. Для краткости оставим справа только слагаемые в скобках:

Теперь выделим последовательно множители в правой части

Замечаем закономерность и записываем окончательно:

С множителем v_at внутри скобок это уравнение имеет вид:

Для исключения ошибок, для проверки точности уравнения выполняем обратное действие, раскрываем скобки:

То же самое для уравнения с множителем v_at внутри скобок:

Видим, что последовательности явно ведут к верному результату. Однако для большей уверенности рассмотрим, как и выше, вариант с числом слагаемых n = 10:

Вновь, заметив закономерность, записываем для n=10:

Проверяем ряд, как и ранее, раскрывая скобки:

Сравниваем этот прямо и обратно преобразованный ряд с исходным рядом слагаемых (10.2):

Видим, что эти ряды для n = 10 совпали, поэтому переписываем правую часть уравнения (10.2) в общем виде:

Или в полном виде:

Здесь число слагаемых (с учётом единичного слагаемого) равно 10. Для произвольного числа слагаемых уравнение (10.1) закономерно можно записать в следующем виде:

То же самое с множителем, внесённым в скобки:

Мы рассматривали движение авто на вытягивающейся дорожке. Однако все приведённые рассуждения полностью соответствуют и движению фотона от некоторой сверхновой к Земле в расширяющемся пространстве Вселенной. Поэтому в итоговых уравнениях мы можем просто заменить скорость авто скоростью света:

Уравнение (10.3) показывает действительную величину удалённости фотонов от сверхновой, равенство (10.4) отражает равенство этой удалённости и конечной удалённости Земли от сверхновой. Это условие мы заложили в постановке задачи. Но из них следует и провозглашённый в задаче вывод. Всё движение, и авто и фотонов, происходило в течение времени T, что соответствует, в свою очередь, длине пройденного пути с точки зрения движущегося объекта – авто или фотонов. Действительно, на спидометре авто за это время при заданной скорости будет показан вполне определённый пройденный им путь: